Solving Problems with Time-dependent Hamiltonians¶
Methods for Writing Time-Dependent Operators¶
In the previous examples of quantum evolution,
we assumed that the systems under consideration were described by time-independent Hamiltonians.
However, many systems have explicit time dependence in either the Hamiltonian,
or the collapse operators describing coupling to the environment, and sometimes both components might depend on time.
The time-evolutions solvers
qutip.mesolve, qutip.mcsolve, qutip.sesolve, qutip.brmesolve
qutip.ssesolve, qutip.photocurrent_sesolve, qutip.smesolve, and qutip.photocurrent_mesolve
are all capable of handling time-dependent Hamiltonians and collapse terms.
There are, in general, three different ways to implement time-dependent problems in QuTiP:
Function based: Hamiltonian / collapse operators expressed using [qobj, func] pairs, where the time-dependent coefficients of the Hamiltonian (or collapse operators) are expressed using Python functions.
String (Cython) based: The Hamiltonian and/or collapse operators are expressed as a list of [qobj, string] pairs, where the time-dependent coefficients are represented as strings. The resulting Hamiltonian is then compiled into C code using Cython and executed.
Array Based: The Hamiltonian and/or collapse operators are expressed as a list of [qobj, np.array] pairs. The arrays are 1 dimensional and dtype are complex or float. They must contain one value for each time in the tlist given to the solver. Cubic spline interpolation will be used between the given times.
Hamiltonian function (outdated): The Hamiltonian is itself a Python function with time-dependence. Collapse operators must be time independent using this input format.
Give the multiple choices of input style, the first question that arrises is which option to choose?
In short, the function based method (option #1) is the most general,
allowing for essentially arbitrary coefficients expressed via user defined functions.
However, by automatically compiling your system into C++ code,
the second option (string based) tends to be more efficient and will run faster
[This is also the only format that is supported in the qutip.brmesolve solver].
Of course, for small system sizes and evolution times, the difference will be minor.
Although this method does not support all time-dependent coefficients that one can think of,
it does support essentially all problems that one would typically encounter.
Time-dependent coefficients using any of the following functions,
or combinations thereof (including constants) can be compiled directly into C++-code:
'abs', 'acos', 'acosh', 'arg', 'asin', 'asinh', 'atan', 'atanh', 'conj',
'cos', 'cosh','exp', 'erf', 'zerf', 'imag', 'log', 'log10', 'norm', 'pi',
'proj', 'real', 'sin', 'sinh', 'sqrt', 'tan', 'tanh'
In addition, QuTiP supports cubic spline based interpolation functions [Modeling Non-Analytic and/or Experimental Time-Dependent Parameters using Interpolating Functions].
If you require mathematical functions other than those listed above,
it is possible to call any of the functions in the NumPy library using the prefix np.
before the function name in the string, i.e 'np.sin(t)' and scipy.special imported as spe.
This includes a wide range of functionality, but comes with a small overhead created by going from C++->Python->C++.
Finally option #4, expressing the Hamiltonian as a Python function, is the original method for time dependence in QuTiP 1.x. However, this method is somewhat less efficient then the previously mentioned methods. However, in contrast to the other options this method can be used in implementing time-dependent Hamiltonians that cannot be expressed as a function of constant operators with time-dependent coefficients.
A collection of examples demonstrating the simulation of time-dependent problems can be found on the tutorials web page.
Function Based Time Dependence¶
A very general way to write a time-dependent Hamiltonian or collapse operator is by using Python functions as the time-dependent coefficients. To accomplish this, we need to write a Python function that returns the time-dependent coefficient. Additionally, we need to tell QuTiP that a given Hamiltonian or collapse operator should be associated with a given Python function. To do this, one needs to specify operator-function pairs in list format: [Op, py_coeff], where Op is a given Hamiltonian or collapse operator and py_coeff is the name of the Python function representing the coefficient. With this format, the form of the Hamiltonian for both mesolve and mcsolve is:
>>> H = [H0, [H1, py_coeff1], [H2, py_coeff2], ...]
where H0 is a time-independent Hamiltonian, while H1,``H2``, are time dependent. The same format can be used for collapse operators:
>>> c_ops = [[C0, py_coeff0], C1, [C2, py_coeff2], ...]
Here we have demonstrated that the ordering of time-dependent and time-independent terms does not matter. In addition, any or all of the collapse operators may be time dependent.
Note
While, in general, you can arrange time-dependent and time-independent terms in any order you like, it is best to place all time-independent terms first.
As an example, we will look at an example that has a time-dependent Hamiltonian of the form \(H=H_{0}-f(t)H_{1}\) where \(f(t)\) is the time-dependent driving strength given as \(f(t)=A\exp\left[-\left( t/\sigma \right)^{2}\right]\). The follow code sets up the problem
ustate = basis(3, 0)
excited = basis(3, 1)
ground = basis(3, 2)
N = 2 # Set where to truncate Fock state for cavity
sigma_ge = tensor(qeye(N), ground * excited.dag()) # |g><e|
sigma_ue = tensor(qeye(N), ustate * excited.dag()) # |u><e|
a = tensor(destroy(N), qeye(3))
ada = tensor(num(N), qeye(3))
c_ops = [] # Build collapse operators
kappa = 1.5 # Cavity decay rate
c_ops.append(np.sqrt(kappa) * a)
gamma = 6 # Atomic decay rate
c_ops.append(np.sqrt(5*gamma/9) * sigma_ue) # Use Rb branching ratio of 5/9 e->u
c_ops.append(np.sqrt(4*gamma/9) * sigma_ge) # 4/9 e->g
t = np.linspace(-15, 15, 100) # Define time vector
psi0 = tensor(basis(N, 0), ustate) # Define initial state
state_GG = tensor(basis(N, 1), ground) # Define states onto which to project
sigma_GG = state_GG * state_GG.dag()
state_UU = tensor(basis(N, 0), ustate)
sigma_UU = state_UU * state_UU.dag()
g = 5 # coupling strength
H0 = -g * (sigma_ge.dag() * a + a.dag() * sigma_ge) # time-independent term
H1 = (sigma_ue.dag() + sigma_ue) # time-dependent term
Given that we have a single time-dependent Hamiltonian term, and constant collapse terms, we need to specify a single Python function for the coefficient \(f(t)\). In this case, one can simply do
def H1_coeff(t, args):
return 9 * np.exp(-(t / 5.) ** 2)
In this case, the return value dependents only on time. However, when specifying Python functions for coefficients, the function must have (t,args) as the input variables, in that order. Having specified our coefficient function, we can now specify the Hamiltonian in list format and call the solver (in this case qutip.mesolve)
H = [H0,[H1, H1_coeff]]
output = mesolve(H, psi0, t, c_ops, [ada, sigma_UU, sigma_GG])
We can call the Monte Carlo solver in the exact same way (if using the default ntraj=500):
output = mcsolve(H, psi0, t, c_ops, [ada, sigma_UU, sigma_GG])
The output from the master equation solver is identical to that shown in the examples, the Monte Carlo however will be noticeably off, suggesting we should increase the number of trajectories for this example. In addition, we can also consider the decay of a simple Harmonic oscillator with time-varying decay rate
kappa = 0.5
def col_coeff(t, args): # coefficient function
return np.sqrt(kappa * np.exp(-t))
N = 10 # number of basis states
a = destroy(N)
H = a.dag() * a # simple HO
psi0 = basis(N, 9) # initial state
c_ops = [[a, col_coeff]] # time-dependent collapse term
times = np.linspace(0, 10, 100)
output = mesolve(H, psi0, times, c_ops, [a.dag() * a])
Using the args variable¶
In the previous example we hardcoded all of the variables, driving amplitude \(A\) and width \(\sigma\), with their numerical values. This is fine for problems that are specialized, or that we only want to run once. However, in many cases, we would like to change the parameters of the problem in only one location (usually at the top of the script), and not have to worry about manually changing the values on each run. QuTiP allows you to accomplish this using the keyword args as an input to the solvers. For instance, instead of explicitly writing 9 for the amplitude and 5 for the width of the gaussian driving term, we can make us of the args variable
def H1_coeff(t, args):
return args['A'] * np.exp(-(t/args['sigma'])**2)
or equivalently,
def H1_coeff(t, args):
A = args['A']
sig = args['sigma']
return A * np.exp(-(t / sig) ** 2)
where args is a Python dictionary of key: value pairs args = {'A': a, 'sigma': b} where a and b are the two parameters for the amplitude and width, respectively. Of course, we can always hardcode the values in the dictionary as well args = {'A': 9, 'sigma': 5}, but there is much more flexibility by using variables in args. To let the solvers know that we have a set of args to pass we append the args to the end of the solver input:
output = mesolve(H, psi0, times, c_ops, [a.dag() * a], args={'A': 9, 'sigma': 5})
or to keep things looking pretty
args = {'A': 9, 'sigma': 5}
output = mesolve(H, psi0, times, c_ops, [a.dag() * a], args=args)
Once again, the Monte Carlo solver qutip.mcsolve works in an identical manner.
String Format Method¶
Note
You must have Cython installed on your computer to use this format. See Installation for instructions on installing Cython.
The string-based time-dependent format works in a similar manner as the previously discussed Python function method. That being said, the underlying code does something completely different. When using this format, the strings used to represent the time-dependent coefficients, as well as Hamiltonian and collapse operators, are rewritten as Cython code using a code generator class and then compiled into C code. The details of this meta-programming will be published in due course. however, in short, this can lead to a substantial reduction in time for complex time-dependent problems, or when simulating over long intervals.
Like the previous method, the string-based format uses a list pair format [Op, str] where str is now a string representing the time-dependent coefficient. For our first example, this string would be '9 * exp(-(t / 5.) ** 2)'. The Hamiltonian in this format would take the form:
ustate = basis(3, 0)
excited = basis(3, 1)
ground = basis(3, 2)
N = 2 # Set where to truncate Fock state for cavity
sigma_ge = tensor(qeye(N), ground * excited.dag()) # |g><e|
sigma_ue = tensor(qeye(N), ustate * excited.dag()) # |u><e|
a = tensor(destroy(N), qeye(3))
ada = tensor(num(N), qeye(3))
c_ops = [] # Build collapse operators
kappa = 1.5 # Cavity decay rate
c_ops.append(np.sqrt(kappa) * a)
gamma = 6 # Atomic decay rate
c_ops.append(np.sqrt(5*gamma/9) * sigma_ue) # Use Rb branching ratio of 5/9 e->u
c_ops.append(np.sqrt(4*gamma/9) * sigma_ge) # 4/9 e->g
t = np.linspace(-15, 15, 100) # Define time vector
psi0 = tensor(basis(N, 0), ustate) # Define initial state
state_GG = tensor(basis(N, 1), ground) # Define states onto which to project
sigma_GG = state_GG * state_GG.dag()
state_UU = tensor(basis(N, 0), ustate)
sigma_UU = state_UU * state_UU.dag()
g = 5 # coupling strength
H0 = -g * (sigma_ge.dag() * a + a.dag() * sigma_ge) # time-independent term
H1 = (sigma_ue.dag() + sigma_ue) # time-dependent term
H = [H0, [H1, '9 * exp(-(t / 5) ** 2)']]
Notice that this is a valid Hamiltonian for the string-based format as exp is included in the above list of suitable functions. Calling the solvers is the same as before:
output = mesolve(H, psi0, t, c_ops, [a.dag() * a])
We can also use the args variable in the same manner as before, however we must rewrite our string term to read: 'A * exp(-(t / sig) ** 2)'
H = [H0, [H1, 'A * exp(-(t / sig) ** 2)']]
args = {'A': 9, 'sig': 5}
output = mesolve(H, psi0, times, c_ops, [a.dag()*a], args=args)
Important
Naming your args variables exp, sin, pi etc. will cause errors when using the string-based format.
Collapse operators are handled in the exact same way.
Modeling Non-Analytic and/or Experimental Time-Dependent Parameters using Interpolating Functions¶
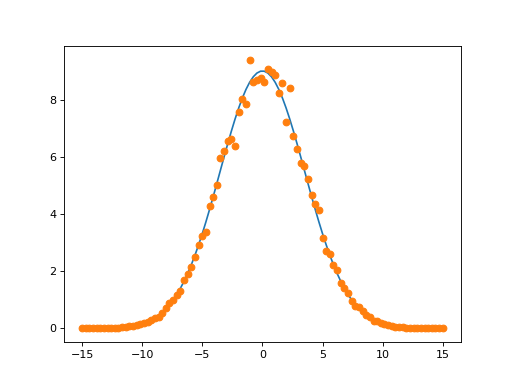
Sometimes it is necessary to model a system where the time-dependent parameters are non-analytic functions, or are derived from experimental data (i.e. a collection of data points). In these situations, one can use interpolating functions as an approximate functional form for input into a time-dependent solver. QuTiP includes it own custom cubic spline interpolation class qutip.interpolate.Cubic_Spline to provide this functionality. To see how this works, lets first generate some noisy data:
t = np.linspace(-15, 15, 100)
func = lambda t: 9*np.exp(-(t / 5)** 2)
noisy_func = lambda t: func(t)+(0.05*func(t))*np.random.randn(t.shape[0])
noisy_data = noisy_func(t)
plt.figure()
plt.plot(t, func(t))
plt.plot(t, noisy_data, 'o')
plt.show()
To turn these data points into a function we call the QuTiP qutip.interpolate.Cubic_Spline class using the first and last domain time points, t[0] and t[-1], respectively, as well as the entire array of data points:
S = Cubic_Spline(t[0], t[-1], noisy_data)
plt.figure()
plt.plot(t, func(t))
plt.plot(t, noisy_data, 'o')
plt.plot(t, S(t), lw=2)
plt.show()
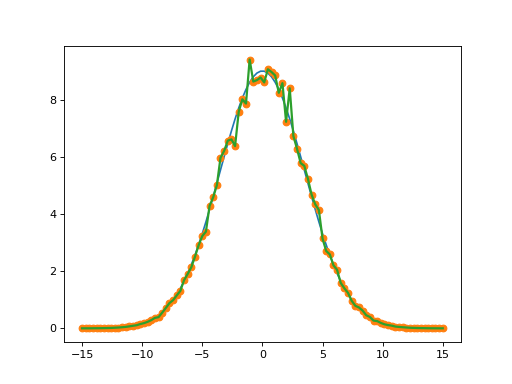
Note that, at present, only equally spaced real or complex data sets can be accommodated. This cubic spline class S can now be pasted to any of the mesolve, mcsolve, or sesolve functions where one would normally input a time-dependent function or string-representation. Taking the problem from the previous section as an example. We would make the replacement:
H = [H0, [H1, '9 * exp(-(t / 5) ** 2)']]
to
H = [H0, [H1, S]]
When combining interpolating functions with other Python functions or strings, the interpolating class will automatically pick the appropriate method for calling the class. That is to say that, if for example, you have other time-dependent terms that are given in the string-format, then the cubic spline representation will also be passed in a string-compatible format. In the string-format, the interpolation function is compiled into c-code, and thus is quite fast. This is the default method if no other time-dependent terms are present.
Accesing the state from solver¶
New in QuTiP 4.4
The state of the system, the ket vector or the density matrix,
is available to time-dependent Hamiltonian and collapse operators in args.
Some keys of the argument dictionary are understood by the solver to be values
to be updated with the evolution of the system.
The state can be obtained in 3 forms: Qobj, vector (1d np.array), matrix (2d np.array),
expectation values and collapse can also be obtained.
Preparation |
usage |
Notes |
|
state as Qobj |
|
|
The ket or density matrix as a Qobj with |
state as matrix |
|
|
The state as a matrix, equivalent to |
state as vector |
|
|
The state as a vector, equivalent to |
expectation value |
|
|
Expectation value of the operator |
collpases |
|
|
List of collapse,
each collapse is a tuple of the pair |
Here psi0 is the initial value used for tests before the evolution begins.
qutip.brmesolve does not support these arguments.
Reusing Time-Dependent Hamiltonian Data¶
Note
This section covers a specialized topic and may be skipped if you are new to QuTiP.
When repeatedly simulating a system where only the time-dependent variables, or initial state change, it is possible to reuse the Hamiltonian data stored in QuTiP and there by avoid spending time needlessly preparing the Hamiltonian and collapse terms for simulation. To turn on the the reuse features, we must pass a qutip.Options object with the rhs_reuse flag turned on. Instructions on setting flags are found in Setting Options for the Dynamics Solvers. For example, we can do
H = [H0, [H1, 'A * exp(-(t / sig) ** 2)']]
args = {'A': 9, 'sig': 5}
output = mcsolve(H, psi0, times, c_ops, [a.dag()*a], args=args)
opts = Options(rhs_reuse=True)
args = {'A': 10, 'sig': 3}
output = mcsolve(H, psi0, times, c_ops, [a.dag()*a], args=args, options=opts)
The second call to qutip.mcsolve does not reorganize the data, and in the case of the string format, does not recompile the Cython code. For the small system here, the savings in computation time is quite small, however, if you need to call the solvers many times for different parameters, this savings will obviously start to add up.
Running String-Based Time-Dependent Problems using Parfor¶
Note
This section covers a specialized topic and may be skipped if you are new to QuTiP.
In this section we discuss running string-based time-dependent problems using the qutip.parfor function. As the qutip.mcsolve function is already parallelized, running string-based time dependent problems inside of parfor loops should be restricted to the qutip.mesolve function only. When using the string-based format, the system Hamiltonian and collapse operators are converted into C code with a specific file name that is automatically genrated, or supplied by the user via the rhs_filename property of the qutip.Options class. Because the qutip.parfor function uses the built-in Python multiprocessing functionality, in calling the solver inside a parfor loop, each thread will try to generate compiled code with the same file name, leading to a crash. To get around this problem you can call the qutip.rhs_generate function to compile simulation into C code before calling parfor. You must then set the qutip.Odedata object rhs_reuse=True for all solver calls inside the parfor loop that indicates that a valid C code file already exists and a new one should not be generated. As an example, we will look at the Landau-Zener-Stuckelberg interferometry example that can be found in the notebook “Time-dependent master equation: Landau-Zener-Stuckelberg inteferometry” in the tutorials section of the QuTiP web site.
To set up the problem, we run the following code:
delta = 0.1 * 2 * np.pi # qubit sigma_x coefficient
w = 2.0 * 2 * np.pi # driving frequency
T = 2 * np.pi / w # driving period
gamma1 = 0.00001 # relaxation rate
gamma2 = 0.005 # dephasing rate
eps_list = np.linspace(-10.0, 10.0, 51) * 2 * np.pi # epsilon
A_list = np.linspace(0.0, 20.0, 51) * 2 * np.pi # Amplitude
sx = sigmax(); sz = sigmaz(); sm = destroy(2); sn = num(2)
c_ops = [np.sqrt(gamma1) * sm, np.sqrt(gamma2) * sz] # relaxation and dephasing
H0 = -delta / 2.0 * sx
H1 = [sz, '-eps / 2.0 + A / 2.0 * sin(w * t)']
H_td = [H0, H1]
Hargs = {'w': w, 'eps': eps_list[0], 'A': A_list[0]}
where the last code block sets up the problem using a string-based Hamiltonian, and Hargs is a dictionary of arguments to be passed into the Hamiltonian. In this example, we are going to use the qutip.propagator and qutip.propagator.propagator_steadystate to find expectation
values for different values of \(\epsilon\) and \(A\) in the
Hamiltonian \(H = -\frac{1}{2}\Delta\sigma_x -\frac{1}{2}\epsilon\sigma_z- \frac{1}{2}A\sin(\omega t)\).
We must now tell the qutip.mesolve function, that is called by qutip.propagator to reuse a
pre-generated Hamiltonian constructed using the qutip.rhs_generate command:
opts = Options(rhs_reuse=True)
rhs_generate(H_td, c_ops, Hargs, name='lz_func')
Here, we have given the generated file a custom name lz_func, however this is not necessary as a generic name will automatically be given. Now we define the function task that is called by qutip.parallel.parfor with the m-index parallelized in loop over the elements of p_mat[m,n]:
def task(args):
m, eps = args
p_mat_m = np.zeros(len(A_list))
for n, A in enumerate(A_list):
# change args sent to solver, w is really a constant though.
Hargs = {'w': w, 'eps': eps,'A': A}
U = propagator(H_td, T, c_ops, Hargs, opts) #<- IMPORTANT LINE
rho_ss = propagator_steadystate(U)
p_mat_m[n] = expect(sn, rho_ss)
return [m, p_mat_m]
Notice the Options opts in the call to the qutip.propagator function. This is tells the qutip.mesolve function used in the propagator to call the pre-generated file lz_func. If this were missing then the routine would fail.