Manipulating States and Operators¶
Introduction¶
In the previous guide section Basic Operations on Quantum Objects, we saw how to create states and operators, using the functions built into QuTiP. In this portion of the guide, we will look at performing basic operations with states and operators. For more detailed demonstrations on how to use and manipulate these objects, see the examples on the tutorials web page.
State Vectors (kets or bras)¶
Here we begin by creating a Fock qutip.states.basis vacuum state vector \(\left|0\right>\) with in a Hilbert space with 5 number states, from 0 to 4:
In [1]: vac = basis(5, 0)
In [2]: vac
Out[2]:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[ 1.]
[ 0.]
[ 0.]
[ 0.]
[ 0.]]
and then create a lowering operator \(\left(\hat{a}\right)\) corresponding to 5 number states using the qutip.operators.destroy function:
In [3]: a = destroy(5)
In [4]: a
Out[4]:
Quantum object: dims = [[5], [5]], shape = (5, 5), type = oper, isherm = False
Qobj data =
[[ 0. 1. 0. 0. 0. ]
[ 0. 0. 1.41421356 0. 0. ]
[ 0. 0. 0. 1.73205081 0. ]
[ 0. 0. 0. 0. 2. ]
[ 0. 0. 0. 0. 0. ]]
Now lets apply the destruction operator to our vacuum state vac,
In [5]: a * vac
Out[5]:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[ 0.]
[ 0.]
[ 0.]
[ 0.]
[ 0.]]
We see that, as expected, the vacuum is transformed to the zero vector. A more interesting example comes from using the adjoint of the lowering operator, the raising operator \(\hat{a}^\dagger\):
In [6]: a.dag() * vac
Out[6]:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[ 0.]
[ 1.]
[ 0.]
[ 0.]
[ 0.]]
The raising operator has in indeed raised the state vec from the vacuum to the \(\left| 1\right>\) state. Instead of using the dagger Qobj.dag() method to raise the state, we could have also used the built in qutip.operators.create function to make a raising operator:
In [7]: c = create(5)
In [8]: c * vac
Out[8]:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[ 0.]
[ 1.]
[ 0.]
[ 0.]
[ 0.]]
which does the same thing. We can raise the vacuum state more than once by successively apply the raising operator:
In [9]: c * c * vac
Out[9]:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[ 0. ]
[ 0. ]
[ 1.41421356]
[ 0. ]
[ 0. ]]
or just taking the square of the raising operator \(\left(\hat{a}^\dagger\right)^{2}\):
In [10]: c ** 2 * vac
Out[10]:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[ 0. ]
[ 0. ]
[ 1.41421356]
[ 0. ]
[ 0. ]]
Applying the raising operator twice gives the expected \(\sqrt{n + 1}\) dependence. We can use the product of \(c * a\) to also apply the number operator to the state vector vac:
In [11]: c * a * vac
Out[11]:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[ 0.]
[ 0.]
[ 0.]
[ 0.]
[ 0.]]
or on the \(\left| 1\right>\) state:
In [12]: c * a * (c * vac)
Out[12]:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[ 0.]
[ 1.]
[ 0.]
[ 0.]
[ 0.]]
or the \(\left| 2\right>\) state:
In [13]: c * a * (c**2 * vac)
Out[13]:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[ 0. ]
[ 0. ]
[ 2.82842712]
[ 0. ]
[ 0. ]]
Notice how in this last example, application of the number operator does not give the expected value \(n=2\), but rather \(2\sqrt{2}\). This is because this last state is not normalized to unity as \(c\left| n\right> = \sqrt{n+1}\left| n+1\right>\). Therefore, we should normalize our vector first:
In [14]: c * a * (c**2 * vac).unit()
Out[14]:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[ 0.]
[ 0.]
[ 2.]
[ 0.]
[ 0.]]
Since we are giving a demonstration of using states and operators, we have done a lot more work than we should have. For example, we do not need to operate on the vacuum state to generate a higher number Fock state. Instead we can use the qutip.states.basis (or qutip.states.fock) function to directly obtain the required state:
In [15]: ket = basis(5, 2)
In [16]: print(ket)
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[ 0.]
[ 0.]
[ 1.]
[ 0.]
[ 0.]]
Notice how it is automatically normalized. We can also use the built in qutip.operators.num operator:
In [17]: n = num(5)
In [18]: print(n)
Quantum object: dims = [[5], [5]], shape = (5, 5), type = oper, isherm = True
Qobj data =
[[ 0. 0. 0. 0. 0.]
[ 0. 1. 0. 0. 0.]
[ 0. 0. 2. 0. 0.]
[ 0. 0. 0. 3. 0.]
[ 0. 0. 0. 0. 4.]]
Therefore, instead of c * a * (c ** 2 * vac).unit() we have:
In [19]: n * ket
Out[19]:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[ 0.]
[ 0.]
[ 2.]
[ 0.]
[ 0.]]
We can also create superpositions of states:
In [20]: ket = (basis(5, 0) + basis(5, 1)).unit()
In [21]: print(ket)
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[ 0.70710678]
[ 0.70710678]
[ 0. ]
[ 0. ]
[ 0. ]]
where we have used the qutip.Qobj.unit method to again normalize the state. Operating with the number function again:
In [22]: n * ket
Out[22]:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[ 0. ]
[ 0.70710678]
[ 0. ]
[ 0. ]
[ 0. ]]
We can also create coherent states and squeezed states by applying the qutip.operators.displace and qutip.operators.squeeze functions to the vacuum state:
In [23]: vac = basis(5, 0)
In [24]: d = displace(5, 1j)
In [25]: s = squeeze(5, 0.25 + 0.25j)
In [26]: d * vac
Out[26]:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[ 0.60655682+0.j ]
[ 0.00000000+0.60628133j]
[-0.43038740+0.j ]
[ 0.00000000-0.24104351j]
[ 0.14552147+0.j ]]
In [27]: d * s * vac
Out[27]:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[ 0.65893786+0.08139381j]
[ 0.10779462+0.51579735j]
[-0.37567217-0.01326853j]
[-0.02688063-0.23828775j]
[ 0.26352814+0.11512178j]]
Of course, displacing the vacuum gives a coherent state, which can also be generated using the built in qutip.states.coherent function.
Density matrices¶
One of the main purpose of QuTiP is to explore the dynamics of open quantum systems, where the most general state of a system is not longer a state vector, but rather a density matrix. Since operations on density matrices operate identically to those of vectors, we will just briefly highlight creating and using these structures.
The simplest density matrix is created by forming the outer-product \(\left|\psi\right>\left<\psi\right|\) of a ket vector:
In [28]: ket = basis(5, 2)
In [29]: ket * ket.dag()
Out[29]:
Quantum object: dims = [[5], [5]], shape = (5, 5), type = oper, isherm = True
Qobj data =
[[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 1. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]]
A similar task can also be accomplished via the qutip.states.fock_dm or qutip.states.ket2dm functions:
In [30]: fock_dm(5, 2)
Out[30]:
Quantum object: dims = [[5], [5]], shape = (5, 5), type = oper, isherm = True
Qobj data =
[[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 1. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]]
In [31]: ket2dm(ket)
Out[31]:
Quantum object: dims = [[5], [5]], shape = (5, 5), type = oper, isherm = True
Qobj data =
[[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 1. 0. 0.]
[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]]
If we want to create a density matrix with equal classical probability of being found in the \(\left|2\right>\) or \(\left|4\right>\) number states we can do the following:
In [32]: 0.5 * ket2dm(basis(5, 4)) + 0.5 * ket2dm(basis(5, 2))
Out[32]:
Quantum object: dims = [[5], [5]], shape = (5, 5), type = oper, isherm = True
Qobj data =
[[ 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. ]
[ 0. 0. 0.5 0. 0. ]
[ 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0.5]]
or use 0.5 * fock_dm(5, 2) + 0.5 * fock_dm(5, 4). There are also several other built-in functions for creating predefined density matrices, for example qutip.states.coherent_dm and qutip.states.thermal_dm which create coherent state and thermal state density matrices, respectively.
In [33]: coherent_dm(5, 1.25)
Out[33]:
Quantum object: dims = [[5], [5]], shape = (5, 5), type = oper, isherm = True
Qobj data =
[[ 0.20980701 0.26141096 0.23509686 0.15572585 0.13390765]
[ 0.26141096 0.32570738 0.29292109 0.19402805 0.16684347]
[ 0.23509686 0.29292109 0.26343512 0.17449684 0.1500487 ]
[ 0.15572585 0.19402805 0.17449684 0.11558499 0.09939079]
[ 0.13390765 0.16684347 0.1500487 0.09939079 0.0854655 ]]
In [34]: thermal_dm(5, 1.25)
Out[34]:
Quantum object: dims = [[5], [5]], shape = (5, 5), type = oper, isherm = True
Qobj data =
[[ 0.46927974 0. 0. 0. 0. ]
[ 0. 0.26071096 0. 0. 0. ]
[ 0. 0. 0.14483942 0. 0. ]
[ 0. 0. 0. 0.08046635 0. ]
[ 0. 0. 0. 0. 0.04470353]]
QuTiP also provides a set of distance metrics for determining how close two density matrix distributions are to each other. Included are the trace distance qutip.metrics.tracedist, fidelity qutip.metrics.fidelity, Hilbert-Schmidt distance qutip.metrics.hilbert_dist, Bures distance qutip.metrics.bures_dist, and Bures angle qutip.metrics.bures_angle.
In [35]: x = coherent_dm(5, 1.25)
In [36]: y = coherent_dm(5, 1.25j) # <-- note the 'j'
In [37]: z = thermal_dm(5, 0.125)
In [38]: fidelity(x, x)
Out[38]: 1.0000000153373552
In [39]: tracedist(y, y)
����������������������������Out[39]: 0.0
We also know that for two pure states, the trace distance (T) and the fidelity (F) are related by \(T = \sqrt{1 - F^{2}}\).
In [40]: tracedist(y, x)
Out[40]: 0.9771565840173289
In [41]: np.sqrt(1 - fidelity(y, x) ** 2)
Out[41]: 0.97715657013879864
For a pure state and a mixed state, \(1 - F^{2} \le T\) which can also be verified:
In [42]: 1 - fidelity(x, z) ** 2
Out[42]: 0.7782890497671208
In [43]: tracedist(x, z)
Out[43]: 0.8559028328862642
Qubit (two-level) systems¶
Having spent a fair amount of time on basis states that represent harmonic oscillator states, we now move on to qubit, or two-level quantum systems (for example a spin-1/2). To create a state vector corresponding to a qubit system, we use the same qutip.states.basis, or qutip.states.fock, function with only two levels:
In [44]: spin = basis(2, 0)
Now at this point one may ask how this state is different than that of a harmonic oscillator in the vacuum state truncated to two energy levels?
In [45]: vac = basis(2, 0)
At this stage, there is no difference. This should not be surprising as we called the exact same function twice. The difference between the two comes from the action of the spin operators qutip.operators.sigmax, qutip.operators.sigmay, qutip.operators.sigmaz, qutip.operators.sigmap, and qutip.operators.sigmam on these two-level states. For example, if vac corresponds to the vacuum state of a harmonic oscillator, then, as we have already seen, we can use the raising operator to get the \(\left|1\right>\) state:
In [46]: vac
Out[46]:
Quantum object: dims = [[2], [1]], shape = (2, 1), type = ket
Qobj data =
[[ 1.]
[ 0.]]
In [47]: c = create(2)
In [48]: c * vac
Out[48]:
Quantum object: dims = [[2], [1]], shape = (2, 1), type = ket
Qobj data =
[[ 0.]
[ 1.]]
For a spin system, the operator analogous to the raising operator is the sigma-plus operator qutip.operators.sigmap. Operating on the spin state gives:
In [49]: spin
Out[49]:
Quantum object: dims = [[2], [1]], shape = (2, 1), type = ket
Qobj data =
[[ 1.]
[ 0.]]
In [50]: sigmap() * spin
���������������������������������������������������������������������������������������������������Out[50]:
Quantum object: dims = [[2], [1]], shape = (2, 1), type = ket
Qobj data =
[[ 0.]
[ 0.]]
Now we see the difference! The qutip.operators.sigmap operator acting on the spin state returns the zero vector. Why is this? To see what happened, let us use the qutip.operators.sigmaz operator:
In [51]: sigmaz()
Out[51]:
Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = True
Qobj data =
[[ 1. 0.]
[ 0. -1.]]
In [52]: sigmaz() * spin
���������������������������������������������������������������������������������������������������������������������������Out[52]:
Quantum object: dims = [[2], [1]], shape = (2, 1), type = ket
Qobj data =
[[ 1.]
[ 0.]]
In [53]: spin2 = basis(2, 1)
In [54]: spin2
Out[54]:
Quantum object: dims = [[2], [1]], shape = (2, 1), type = ket
Qobj data =
[[ 0.]
[ 1.]]
In [55]: sigmaz() * spin2
���������������������������������������������������������������������������������������������������Out[55]:
Quantum object: dims = [[2], [1]], shape = (2, 1), type = ket
Qobj data =
[[ 0.]
[-1.]]
The answer is now apparent. Since the QuTiP qutip.operators.sigmaz function uses the standard z-basis representation of the sigma-z spin operator, the spin state corresponds to the \(\left|\uparrow\right>\) state of a two-level spin system while spin2 gives the \(\left|\downarrow\right>\) state. Therefore, in our previous example sigmap() * spin, we raised the qubit state out of the truncated two-level Hilbert space resulting in the zero state.
While at first glance this convention might seem somewhat odd, it is in fact quite handy. For one, the spin operators remain in the conventional form. Second, when the spin system is in the \(\left|\uparrow\right>\) state:
In [56]: sigmaz() * spin
Out[56]:
Quantum object: dims = [[2], [1]], shape = (2, 1), type = ket
Qobj data =
[[ 1.]
[ 0.]]
the non-zero component is the zeroth-element of the underlying matrix (remember that python uses c-indexing, and matrices start with the zeroth element). The \(\left|\downarrow\right>\) state therefore has a non-zero entry in the first index position. This corresponds nicely with the quantum information definitions of qubit states, where the excited \(\left|\uparrow\right>\) state is label as \(\left|0\right>\), and the \(\left|\downarrow\right>\) state by \(\left|1\right>\).
If one wants to create spin operators for higher spin systems, then the qutip.operators.jmat function comes in handy.
Expectation values¶
Some of the most important information about quantum systems comes from calculating the expectation value of operators, both Hermitian and non-Hermitian, as the state or density matrix of the system varies in time. Therefore, in this section we demonstrate the use of the qutip.expect function. To begin:
In [57]: vac = basis(5, 0)
In [58]: one = basis(5, 1)
In [59]: c = create(5)
In [60]: N = num(5)
In [61]: expect(N, vac)
Out[61]: 0.0
In [62]: expect(N, one)
�������������Out[62]: 1.0
In [63]: coh = coherent_dm(5, 1.0j)
In [64]: expect(N, coh)
Out[64]: 0.99705557458066
In [65]: cat = (basis(5, 4) + 1.0j * basis(5, 3)).unit()
In [66]: expect(c, cat)
Out[66]: 0.9999999999999998j
The qutip.expect function also accepts lists or arrays of state vectors or density matrices for the second input:
In [67]: states = [(c**k * vac).unit() for k in range(5)] # must normalize
In [68]: expect(N, states)
Out[68]: array([ 0., 1., 2., 3., 4.])
In [69]: cat_list = [(basis(5, 4) + x * basis(5, 3)).unit()
....: for x in [0, 1.0j, -1.0, -1.0j]]
....:
In [70]: expect(c, cat_list)
Out[70]: array([ 0.+0.j, 0.+1.j, -1.+0.j, 0.-1.j])
Notice how in this last example, all of the return values are complex numbers. This is because the qutip.expect function looks to see whether the operator is Hermitian or not. If the operator is Hermitian, than the output will always be real. In the case of non-Hermitian operators, the return values may be complex. Therefore, the qutip.expect function will return an array of complex values for non-Hermitian operators when the input is a list/array of states or density matrices.
Of course, the qutip.expect function works for spin states and operators:
In [71]: up = basis(2, 0)
In [72]: down = basis(2, 1)
In [73]: expect(sigmaz(), up)
Out[73]: 1.0
In [74]: expect(sigmaz(), down)
�������������Out[74]: -1.0
as well as the composite objects discussed in the next section Using Tensor Products and Partial Traces:
In [75]: spin1 = basis(2, 0)
In [76]: spin2 = basis(2, 1)
In [77]: two_spins = tensor(spin1, spin2)
In [78]: sz1 = tensor(sigmaz(), qeye(2))
In [79]: sz2 = tensor(qeye(2), sigmaz())
In [80]: expect(sz1, two_spins)
Out[80]: 1.0
In [81]: expect(sz2, two_spins)
�������������Out[81]: -1.0
Superoperators and Vectorized Operators¶
In addition to state vectors and density operators, QuTiP allows for representing maps that act linearly on density operators using the Kraus, Liouville supermatrix and Choi matrix formalisms. This support is based on the correspondance between linear operators acting on a Hilbert space, and vectors in two copies of that Hilbert space, \(\mathrm{vec} : \mathcal{L}(\mathcal{H}) \to \mathcal{H} \otimes \mathcal{H}\) [Hav03], [Wat13].
This isomorphism is implemented in QuTiP by the
operator_to_vector and
vector_to_operator functions:
In [82]: psi = basis(2, 0)
In [83]: rho = ket2dm(psi)
In [84]: rho
Out[84]:
Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = True
Qobj data =
[[ 1. 0.]
[ 0. 0.]]
In [85]: vec_rho = operator_to_vector(rho)
In [86]: vec_rho
Out[86]:
Quantum object: dims = [[[2], [2]], [1]], shape = (4, 1), type = operator-ket
Qobj data =
[[ 1.]
[ 0.]
[ 0.]
[ 0.]]
In [87]: rho2 = vector_to_operator(vec_rho)
In [88]: (rho - rho2).norm()
Out[88]: 0.0
The type attribute indicates whether a quantum object is
a vector corresponding to an operator (operator-ket), or its Hermitian
conjugate (operator-bra).
Note that QuTiP uses the column-stacking convention for the isomorphism between \(\mathcal{L}(\mathcal{H})\) and \(\mathcal{H} \otimes \mathcal{H}\):
In [89]: import numpy as np
In [90]: A = Qobj(np.arange(4).reshape((2, 2)))
In [91]: A
Out[91]:
Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = False
Qobj data =
[[ 0. 1.]
[ 2. 3.]]
In [92]: operator_to_vector(A)
����������������������������������������������������������������������������������������������������������������������������Out[92]:
Quantum object: dims = [[[2], [2]], [1]], shape = (4, 1), type = operator-ket
Qobj data =
[[ 0.]
[ 2.]
[ 1.]
[ 3.]]
Since \(\mathcal{H} \otimes \mathcal{H}\) is a vector space, linear maps
on this space can be represented as matrices, often called superoperators.
Using the Qobj, the spre and spost functions, supermatrices
corresponding to left- and right-multiplication respectively can be quickly
constructed.
In [93]: X = sigmax()
In [94]: S = spre(X) * spost(X.dag()) # Represents conjugation by X.
Note that this is done automatically by the to_super function when given
type='oper' input.
In [95]: S2 = to_super(X)
In [96]: (S - S2).norm()
Out[96]: 0.0
Quantum objects representing superoperators are denoted by type='super':
In [97]: S
Out[97]:
Quantum object: dims = [[[2], [2]], [[2], [2]]], shape = (4, 4), type = super, isherm = True
Qobj data =
[[ 0. 0. 0. 1.]
[ 0. 0. 1. 0.]
[ 0. 1. 0. 0.]
[ 1. 0. 0. 0.]]
Information about superoperators, such as whether they represent completely
positive maps, is exposed through the iscp, istp
and iscptp attributes:
In [98]: S.iscp, S.istp, S.iscptp
Out[98]: (True, True, True)
In addition, dynamical generators on this extended space, often called
Liouvillian superoperators, can be created using the liouvillian function. Each of these takes a Hamilonian along with
a list of collapse operators, and returns a type="super" object that can
be exponentiated to find the superoperator for that evolution.
In [99]: H = 10 * sigmaz()
In [100]: c1 = destroy(2)
In [101]: L = liouvillian(H, [c1])
In [102]: L
Out[102]:
Quantum object: dims = [[[2], [2]], [[2], [2]]], shape = (4, 4), type = super, isherm = False
Qobj data =
[[ 0.0 +0.j 0.0 +0.j 0.0 +0.j 1.0 +0.j]
[ 0.0 +0.j -0.5+20.j 0.0 +0.j 0.0 +0.j]
[ 0.0 +0.j 0.0 +0.j -0.5-20.j 0.0 +0.j]
[ 0.0 +0.j 0.0 +0.j 0.0 +0.j -1.0 +0.j]]
In [103]: S = (12 * L).expm()
For qubits, a particularly useful way to visualize superoperators is to plot them in the Pauli basis, such that \(S_{\mu,\nu} = \langle\!\langle \sigma_{\mu} | S[\sigma_{\nu}] \rangle\!\rangle\). Because the Pauli basis is Hermitian, \(S_{\mu,\nu}\) is a real number for all Hermitian-preserving superoperators \(S\), allowing us to plot the elements of \(S\) as a Hinton diagram. In such diagrams, positive elements are indicated by white squares, and negative elements by black squares. The size of each element is indicated by the size of the corresponding square. For instance, let \(S[\rho] = \sigma_x \rho \sigma_x^{\dagger}\). Then \(S[\sigma_{\mu}] = \sigma_{\mu} \cdot \begin{cases} +1 & \mu = 0, x \\ -1 & \mu = y, z \end{cases}\). We can quickly see this by noting that the \(Y\) and \(Z\) elements of the Hinton diagram for \(S\) are negative:
(Source code, png, hires.png, pdf)
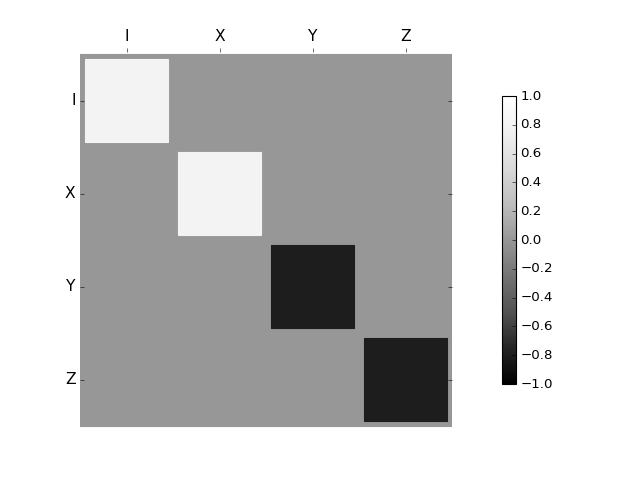
Choi, Kraus, Stinespring and \(\chi\) Representations¶
In addition to the superoperator representation of quantum maps, QuTiP supports several other useful representations. First, the Choi matrix \(J(\Lambda)\) of a quantum map \(\Lambda\) is useful for working with ancilla-assisted process tomography (AAPT), and for reasoning about properties of a map or channel. Up to normalization, the Choi matrix is defined by acting \(\Lambda\) on half of an entangled pair. In the column-stacking convention,
In QuTiP, \(J(\Lambda)\) can be found by calling the to_choi
function on a type="super" Qobj.
In [104]: X = sigmax()
In [105]: S = sprepost(X, X)
In [106]: J = to_choi(S)
In [107]: print(J)
Quantum object: dims = [[[2], [2]], [[2], [2]]], shape = (4, 4), type = super, isherm = True, superrep = choi
Qobj data =
[[ 0. 0. 0. 0.]
[ 0. 1. 1. 0.]
[ 0. 1. 1. 0.]
[ 0. 0. 0. 0.]]
In [108]: print(to_choi(spre(qeye(2))))
�������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������Quantum object: dims = [[[2], [2]], [[2], [2]]], shape = (4, 4), type = super, isherm = True, superrep = choi
Qobj data =
[[ 1. 0. 0. 1.]
[ 0. 0. 0. 0.]
[ 0. 0. 0. 0.]
[ 1. 0. 0. 1.]]
If a Qobj instance is already in the Choi superrep, then calling to_choi
does nothing:
In [109]: print(to_choi(J))
Quantum object: dims = [[[2], [2]], [[2], [2]]], shape = (4, 4), type = super, isherm = True, superrep = choi
Qobj data =
[[ 0. 0. 0. 0.]
[ 0. 1. 1. 0.]
[ 0. 1. 1. 0.]
[ 0. 0. 0. 0.]]
To get back to the superoperator representation, simply use the to_super function.
As with to_choi, to_super is idempotent:
In [110]: print(to_super(J) - S)
Quantum object: dims = [[[2], [2]], [[2], [2]]], shape = (4, 4), type = super, isherm = True
Qobj data =
[[ 0. 0. 0. 0.]
[ 0. 0. 0. 0.]
[ 0. 0. 0. 0.]
[ 0. 0. 0. 0.]]
In [111]: print(to_super(S))
��������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������Quantum object: dims = [[[2], [2]], [[2], [2]]], shape = (4, 4), type = super, isherm = True
Qobj data =
[[ 0. 0. 0. 1.]
[ 0. 0. 1. 0.]
[ 0. 1. 0. 0.]
[ 1. 0. 0. 0.]]
We can quickly obtain another useful representation from the Choi matrix by taking its eigendecomposition. In particular, let \(\{A_i\}\) be a set of operators such that \(J(\Lambda) = \sum_i |A_i\rangle\!\rangle \langle\!\langle A_i|\). We can write \(J(\Lambda)\) in this way for any hermicity-preserving map; that is, for any map \(\Lambda\) such that \(J(\Lambda) = J^\dagger(\Lambda)\). These operators then form the Kraus representation of \(\Lambda\). In particular, for any input \(\rho\),
Notice using the column-stacking identity that \((C^\mathrm{T} \otimes A) |B\rangle\!\rangle = |ABC\rangle\!\rangle\), we have that
The Kraus representation of a hermicity-preserving map can be found in QuTiP
using the to_kraus function.
In [112]: I, X, Y, Z = qeye(2), sigmax(), sigmay(), sigmaz()
In [113]: S = sum(sprepost(P, P) for P in (I, X, Y, Z)) / 4
.....: print(S)
.....:
Quantum object: dims = [[[2], [2]], [[2], [2]]], shape = (4, 4), type = super, isherm = True
Qobj data =
[[ 0.5 0. 0. 0.5]
[ 0. 0. 0. 0. ]
[ 0. 0. 0. 0. ]
[ 0.5 0. 0. 0.5]]
In [115]: J = to_choi(S)
.....: print(J)
.....:
������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������Quantum object: dims = [[[2], [2]], [[2], [2]]], shape = (4, 4), type = super, isherm = True, superrep = choi
Qobj data =
[[ 0.5 0. 0. 0. ]
[ 0. 0.5 0. 0. ]
[ 0. 0. 0.5 0. ]
[ 0. 0. 0. 0.5]]
In [117]: print(J.eigenstates()[1])
�����������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������[ Quantum object: dims = [[[2], [2]], [1, 1]], shape = (4, 1), type = operator-ket
Qobj data =
[[ 1.]
[ 0.]
[ 0.]
[ 0.]]
Quantum object: dims = [[[2], [2]], [1, 1]], shape = (4, 1), type = operator-ket
Qobj data =
[[ 0.]
[ 1.]
[ 0.]
[ 0.]]
Quantum object: dims = [[[2], [2]], [1, 1]], shape = (4, 1), type = operator-ket
Qobj data =
[[ 0.]
[ 0.]
[ 1.]
[ 0.]]
Quantum object: dims = [[[2], [2]], [1, 1]], shape = (4, 1), type = operator-ket
Qobj data =
[[ 0.]
[ 0.]
[ 0.]
[ 1.]]]
In [118]: K = to_kraus(S)
.....: print(K)
.....:
�������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������[Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = True
Qobj data =
[[ 0.70710678 0. ]
[ 0. 0. ]], Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = False
Qobj data =
[[ 0. 0. ]
[ 0.70710678 0. ]], Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = False
Qobj data =
[[ 0. 0.70710678]
[ 0. 0. ]], Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = True
Qobj data =
[[ 0. 0. ]
[ 0. 0.70710678]]]
As with the other representation conversion functions, to_kraus
checks the superrep attribute of its input, and chooses an appropriate
conversion method. Thus, in the above example, we can also call to_kraus
on J.
In [120]: KJ = to_kraus(J)
.....: print(KJ)
.....:
[Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = True
Qobj data =
[[ 0.70710678 0. ]
[ 0. 0. ]], Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = False
Qobj data =
[[ 0. 0. ]
[ 0.70710678 0. ]], Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = False
Qobj data =
[[ 0. 0.70710678]
[ 0. 0. ]], Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = True
Qobj data =
[[ 0. 0. ]
[ 0. 0.70710678]]]
In [122]: for A, AJ in zip(K, KJ):
.....: print(A - AJ)
.....:
�����������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = True
Qobj data =
[[ 0. 0.]
[ 0. 0.]]
Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = True
Qobj data =
[[ 0. 0.]
[ 0. 0.]]
Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = True
Qobj data =
[[ 0. 0.]
[ 0. 0.]]
Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = True
Qobj data =
[[ 0. 0.]
[ 0. 0.]]
The Stinespring representation is closely related to the Kraus representation, and consists of a pair of operators \(A\) and \(B\) such that for all operators \(X\) acting on \(\mathcal{H}\),
where the partial trace is over a new index that corresponds to the
index in the Kraus summation. Conversion to Stinespring
is handled by the to_stinespring
function.
In [123]: a = create(2).dag()
In [124]: S_ad = sprepost(a * a.dag(), a * a.dag()) + sprepost(a, a.dag())
.....: S = 0.9 * sprepost(I, I) + 0.1 * S_ad
.....: print(S)
.....:
Quantum object: dims = [[[2], [2]], [[2], [2]]], shape = (4, 4), type = super, isherm = False
Qobj data =
[[ 1. 0. 0. 0.1]
[ 0. 0.9 0. 0. ]
[ 0. 0. 0.9 0. ]
[ 0. 0. 0. 0.9]]
In [127]: A, B = to_stinespring(S)
.....: print(A)
.....: print(B)
.....:
�������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������Quantum object: dims = [[2, 3], [2]], shape = (6, 2), type = other
Qobj data =
[[-0.98845443 0. ]
[ 0. 0.31622777]
[ 0.15151842 0. ]
[ 0. -0.93506452]
[ 0. 0. ]
[ 0. -0.16016975]]
Quantum object: dims = [[2, 3], [2]], shape = (6, 2), type = other
Qobj data =
[[-0.98845443 0. ]
[ 0. 0.31622777]
[ 0.15151842 0. ]
[ 0. -0.93506452]
[ 0. 0. ]
[ 0. -0.16016975]]
Notice that a new index has been added, such that \(A\) and \(B\)
have dimensions [[2, 3], [2]], with the length-3 index representing the
fact that the Choi matrix is rank-3 (alternatively, that the map has three
Kraus operators).
In [130]: to_kraus(S)
Out[130]:
[Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = True
Qobj data =
[[ 0.98845443 0. ]
[ 0. 0.93506452]],
Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = True
Qobj data =
[[-0.15151842 0. ]
[ 0. 0.16016975]],
Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = True
Qobj data =
[[ 0. 0.]
[ 0. 0.]],
Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = False
Qobj data =
[[ 0. 0.31622777]
[ 0. 0. ]]]
In [131]: print(to_choi(S).eigenenergies())
����������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������[ 0. 0.04861218 0.1 1.85138782]
Finally, the last superoperator representation supported by QuTiP is the \(\chi\)-matrix representation,
where \(\{B_\alpha\}\) is a basis for the space of matrices acting
on \(\mathcal{H}\). In QuTiP, this basis is taken to be the Pauli
basis \(B_\alpha = \sigma_\alpha / \sqrt{2}\). Conversion to the
\(\chi\) formalism is handled by the to_chi
function.
In [132]: chi = to_chi(S)
.....: print(chi)
.....:
Quantum object: dims = [[[2], [2]], [[2], [2]]], shape = (4, 4), type = super, isherm = True, superrep = chi
Qobj data =
[[ 3.7+0.j 0.0+0.j 0.0+0.j 0.1+0.j ]
[ 0.0+0.j 0.1+0.j 0.0+0.1j 0.0+0.j ]
[ 0.0+0.j 0.0-0.1j 0.1+0.j 0.0+0.j ]
[ 0.1+0.j 0.0+0.j 0.0+0.j 0.1+0.j ]]
One convenient property of the \(\chi\) matrix is that the average gate fidelity with the identity map can be read off directly from the \(\chi_{00}\) element:
In [134]: print(average_gate_fidelity(S))
0.95
In [135]: print(chi[0, 0] / 4)
�����(0.925+0j)
Here, the factor of 4 comes from the dimension of the underlying
Hilbert space \(\mathcal{H}\). As with the superoperator
and Choi representations, the \(\chi\) representation is
denoted by the superrep, such that to_super,
to_choi, to_kraus,
to_stinespring and to_chi
all convert from the \(\chi\) representation appropriately.
Properties of Quantum Maps¶
In addition to converting between the different representations of quantum maps,
QuTiP also provides attributes to make it easy to check if a map is completely
positive, trace preserving and/or hermicity preserving. Each of these attributes
uses superrep to automatically perform any needed conversions.
In particular, a quantum map is said to be positive (but not necessarily completely positive) if it maps all positive operators to positive operators. For instance, the transpose map \(\Lambda(\rho) = \rho^{\mathrm{T}}\) is a positive map. We run into problems, however, if we tensor \(\Lambda\) with the identity to get a partial transpose map.
In [136]: rho = ket2dm(bell_state())
In [137]: rho_out = partial_transpose(rho, [0, 1])
.....: print(rho_out.eigenenergies())
.....:
[-0.5 0.5 0.5 0.5]
Notice that even though we started with a positive map, we got an operator out
with negative eigenvalues. Complete positivity addresses this by requiring that
a map returns positive operators for all positive operators, and does so even
under tensoring with another map. The Choi matrix is very useful here, as it
can be shown that a map is completely positive if and only if its Choi matrix
is positive [Wat13]. QuTiP implements this check with the iscp
attribute. As an example, notice that the snippet above already calculates
the Choi matrix of the transpose map by acting it on half of an entangled
pair. We simply need to manually set the dims and superrep attributes to reflect the
structure of the underlying Hilbert space and the chosen representation.
In [139]: J = rho_out
In [140]: J.dims = [[[2], [2]], [[2], [2]]]
.....: J.superrep = 'choi'
.....:
In [142]: print(J.iscp)
False
This confirms that the transpose map is not completely positive. On the other hand,
the transpose map does satisfy a weaker condition, namely that it is hermicity preserving.
That is, \(\Lambda(\rho) = (\Lambda(\rho))^\dagger\) for all \(\rho\) such that
\(\rho = \rho^\dagger\). To see this, we note that \((\rho^{\mathrm{T}})^\dagger
= \rho^*\), the complex conjugate of \(\rho\). By assumption, \(\rho = \rho^\dagger
= (\rho^*)^{\mathrm{T}}\), though, such that \(\Lambda(\rho) = \Lambda(\rho^\dagger) = \rho^*\).
We can confirm this by checking the ishp attribute:
In [143]: print(J.ishp)
True
Next, we note that the transpose map does preserve the trace of its inputs, such that
\(\operatorname{Tr}(\Lambda[\rho]) = \operatorname{Tr}(\rho)\) for all \(\rho\).
This can be confirmed by the istp attribute:
In [144]: print(J.ishp)
True
Finally, a map is called a quantum channel if it always maps valid states to valid states. Formally, a map is a channel if it is both completely positive and trace preserving. Thus, QuTiP provides a single attribute to quickly check that this is true.
In [145]: print(J.iscptp)
False
In [146]: print(to_super(qeye(2)).iscptp)
������True